SNP Simulations
Spherical Neutron Polarimetry simulations
The polarisation vector of a neutron beam can be seen as a classical vector in the space of the laboratory. In particular, the component Pα in the direction α is defined as Pα = (n+ - n-) / (n+ + n-) where n+ and n- are the number of neutrons which fall in the |+½> and |-½> eigenstates of the angular momentum component σα of the neutron.
In the 1960s, Izyumov and Maleyev [I62], Blume [B63,B64], Izyumov [I63] and Schermer and Blume [S68] derived the theory of polarised neutrons scattered by various materials using the density matrix formalism within the Born approximation. The theoretical results gave the expressions for the total cross-section σ and the final polarisation vector Ρ summarised in the table below. In these expressions, N is the nuclear structure factor, M is the magnetic interaction vector ki and kf are respectively the incident and final amplitudes of the neutron wave vectors, and Ρi is the incident polarisation vector.
From these equations, one can predict the rotation of the polarisation vector upon scattering. The polarisation direction is conserved when the scattering is of coherent nuclear origin: for example a nuclear Bragg peak without nuclear spin polarisation or an isolated phonon. The polarisation rotates by 180° around the magnetic interaction vector when the interaction is magnetic and non chiral: for example a magnetic satellite of a collinear arrangement or a magnon. For a non-collinear magnetic structure, the intensity may depend on the incident polarisation Ρi and for an helix there is a creation of polarisation along the scattering vector. When there is nuclear-magnetic interference, the intensity depends on Ρi only when Ν and Μ are in phase. As regards the polarisation vector, it rotates toward or around the magnetic interaction vector when Ν and Μ are respectively in phase or in quadrature.
Because the neutron beam polarisation can be considered as a three-dimensional vector, it is obviously useful to define a set of orthogonal polarisation axes on the instrument. Because the magnetic interaction vector Μ is the projection of the magnetic structure factor onto a plane perpendicular to the scattering vector Q, it is convenient to choose X parallel to Q. Z is conventionally chosen perpendicular to the scattering plane and Y completes the right-handed cartesian set.
From the above table, it has already been shown by P.J. Brown [B01] that the scattered polarisation is the combination of a rotation of Ρi with a creation of polarisation:
The 9 components Rαβ and the 3 components Ρα where (α,β) are X, Y, Z indices are obtained by measuring the three components of the scattered polarisation for Ρi = 0, X, Y and Z. The expressions of these 12 quantities are the following in polarisation coordinates:
with:
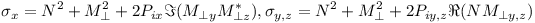
We propose a series of simulations presenting the way the neutron polarisation vector rotates upon scattering. These simulations have been calculated with Mathematica from the Blume - Maleyev equations cited above. Click on the right menu to view your case of interest.
[I62] Y. Izyumov and S. Maleyev Soviet Phys. - JETP 14 (1962) 1668
[B63] M. Blume Phys. Rev.130 (1963) 1670
[B64] M. Blume Phys. Rev.133 (1964) A1366
[I63] Y. Izyumov Soviet Phys. - Usp.16 (1963) 359
[S68] R. Schermer and M. Blume Phys. Rev. 166 (1968) 554
[B01] P.J. Brown, Physica B297 (2001) 198


 (png - 3.21 Ki)
(png - 3.21 Ki)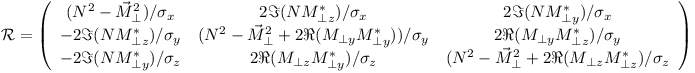
 (png - 4.65 Ki)
(png - 4.65 Ki)