Kicking a curve with magic nuclei leads to a win for nuclear fission
Even as we are going to celebrate 80 years since the discovery of nuclear fission, there remain significant gaps in our understanding of the nuclear fission process – which impacts on the success of modelling the fission reaction and its applications. Despite tremendous effort, aspects of nuclear fission are still open to inquiry.
Nuclear reactors have already been in successful operation for 75 years without a complete understanding of the microscopic processes underpinning fission. In the early day’s novel reactor types were first constructed and operated as prototypes, similar to the early development of cars and airplanes. Nowadays advancements across manufacturing and construction are made using the analysis of very detailed simulations, well before any physical object is made. However, these simulations are only as good as the quality of the input data, so it is imperative we improve our knowledge in order to develop better models and simulations.
A collaboration between the Institut Laue Langevin (ILL), the French Alternative Energies and Atomic Energy Commission (CEA) and the National Centre for Scientific Research (CNRS) has performed experiments to better understand the generation of fission fragment angular momentum.
Nuclear fission consists in splitting a nucleus into (generally two) smaller nuclei, called fission fragments. In the macroscopic world angular momentum can be understood as the spinning of a body around one of its axes. Atomic nuclei come in different shapes: spherical like footballs, longitudinally deformed like rugby balls, pear-like, and so on. So-called doubly magic nuclei tend to be perfectly spherical and stay that way even when excited. Trying to make a perfectly round football spin rapidly (as when a curving cross is kicked) is harder to achieve than giving a spin to a rugby ball, due to its shape. This fundamental problem remains when translating the situation to a microscopic scale, with atomic nuclei. Just as footballs and rugby balls spin differently around their axes due to their shapes, nuclei of different shapes need to be considered differently in fission models.
Understanding the angular momentum of these fission fragments is important as it relates to the number of gamma rays emitted in the process of nuclear fission. In a nuclear fission reactor, these gamma rays are largely responsible for heating and damage made to structural materials. This makes it essential that these features are appropriately accounted for in models and simulations.
A particularly intriguing feature of nuclear fission according to existing models, is that perfectly spherical nuclei like the doubly magic nucleus Sn-132 should not receive angular momentum in the fission process. To ensure this phenomenon is appropriately addressed in future, the collaborators looked for the first time to physically measure the isomeric ratios of the doubly magic nucleus Sn-132 as function of its kinetic energy. In nuclear physics, an isomeric state is a nuclear state with a half-life longer than its neighbouring states. The isomeric ratio corresponds to the number of isomeric states populated over the total number of a given fission fragment.
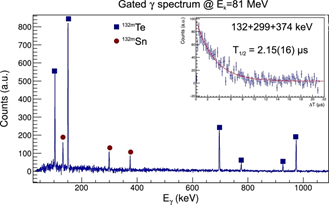
To identify the isomeric state population as a function of kinetic energy, the authors used the LOHENGRIN recoil mass separator at the ILL. This instrument was chosen because of its globally unique capabilities. A modern version of the machine J.J. Thomson used to discover isotopes over a century ago, this instrument is able to separate fission fragments by mass and energy, allowing us to effectively observe and analyse their decay. The group measured some gamma rays specific to the decay of this nuclear state using high purity germanium detectors (see Fig 1). As the energy and intensity of gamma rays are unique for each nuclear state, this acts as a fingerprint for the nucleus and allows deriving the isomeric ratio.
The measured isomeric ratio was then compared with calculations from a de-excitation code named FIFRELIN, which, from an arbitrary initial nuclear state, will decay until reaching the isomeric state or the fundamental state of the Sn-132.
This comparison is shown on Fig 2 (jpg - 234 Ki) where the warmer the colour, the better the agreement is, while Fig 3 (jpg - 74 Ki) shows both the measured isomeric ratios and the derived average angular momentum.
From this it can be observed that the derived average angular momentum is dependent on the fission fragment kinetic energy and is around 4ℏ, where ℏ stands for the smallest possible unit of angular momentum of a quantum mechanical system.
Therefore, the project showed discrepancies with models that have suggested a perfectly spherical nuclei has a spin of near null. This result sets a new benchmark that fission models need to explain, in order to facilitate trustworthy predictions for other fission fragments and other nuclear fission reactions and their parameters in future.
Re.: A. Chebboubi et al., Phys. Lett. B775 (2017) 190.
DOI 10.1016/j.physletb.2017.10.067
Contact: Ulli Köster (ILL), Abdelhazize Chebboubi (CEA)
|  (jpg - 234 Ki) (jpg - 234 Ki) |
| ||
Figure 1: γ spectrum recorded on the LOHENGRIN spectrometer. Specific γ-rays allow identifying unambiguously the isomeric state of the Sn-132. Other γ-rays are those of Te-132 since the LOHENGRIN spectrometer selects only the mass (here 132) and not the nuclear charge of fission fragments | Figure 2: Comparison between FIFRELIN calculations and experimental isomeric ratios. The higher the Bayesian indicator, the better is the agreement. | Figure 3: (top) Measured isomeric ratios as a function of the fission fragment kinetic energy. (bottom) Derived averaged angular momentum as a function of the fission fragment kinetic energy |

 (jpg - 59 Ki)
(jpg - 59 Ki)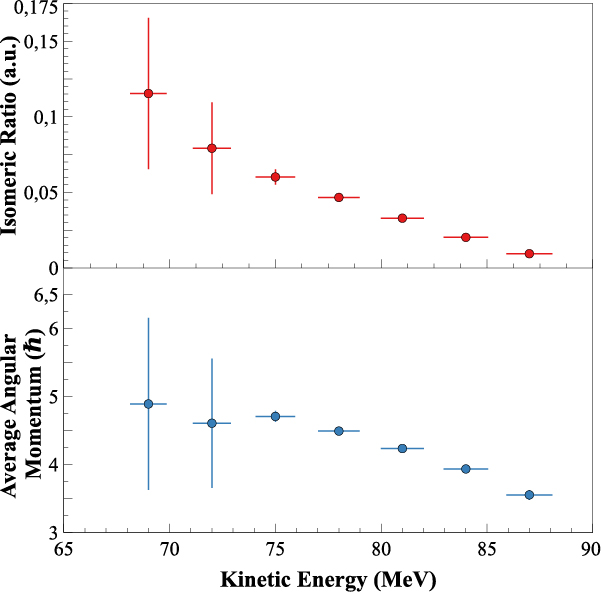 (jpg - 74 Ki)
(jpg - 74 Ki)