Doubts about multiband superconductivity? D33 can fix it!

Recently published findings from experiments carried out at the Institut Laue-Langevin (ILL) and the Swiss Spallation Neutron Source (SINQ) confirm monochromatic small-angle neutron scattering (SANS) as the definitive go-to method to characterise multiband superconductivity in a material.

Superconductivity describes the extraordinary ability of certain materials to conduct an electric current with zero resistance and thus no energy loss. Applications are limited, however, by the need to cool most superconducting materials to extreme temperatures. The discovery of superconductivity in the rather simple binary compound magnesium diboride (MgB₂) at a relatively high transition temperature of 39K (-234.15^oC) ignited significant interest due to the existence of multiple energy bands, that deviate from the single-band model of conventional theory. Could multiband materials unlock a path to new high temperature superconductors?

“There had been some hints that niobium diselenide (2H-NbSe₂) could also be a multiband superconductor, though another group had recently dismissed the two-band picture, arguing instead for an anisotropic single-band model,” explains Ahmed Alshemi, postdoctoral researcher at Lund University and first author of the paper. “We decided to use SANS to find out!”

Indeed, the two-band superconductivity of MgB₂ was demonstrated by SANS experiments carried out at the ILL and published in 2003 by ILL research scientist Robert ‘Bob’ Cubitt. “SANS is an extremely powerful technique,” explains Cubitt. “Whenever any new superconductor turns up, SANS is one of the most definitive and convincing experiments that can be carried out.” The incident neutron beam is scattered by the sample and produces a diffraction pattern that provides precise information about the microscopic symmetries of the superconducting state with respect to temperature and magnetic field strength.

“You obtain these very clear and distinctive Bragg peaks, whose intensities tell you all sorts of crucial things about what's going on inside these superconductors,” explains Cubitt. “Though certain features can be explored using other techniques, such as scanning tunnelling microscopy, the results obtained are more open to interpretation, making it more difficult to rule out alternative explanations,” explains Elizabeth Blackburn, professor at Lund University.

“With MgB₂ we had a bit of luck because the two superconducting bands have different strengths and physical shapes,” explains Cubitt. “Each band is equivalent to a bucket of electrons and the neutron intensity we see basically represents how many electrons from each band are contributing to the overall superconducting state. As we increased the magnetic field, we could see that the contribution from one band was suppressed and that the resulting pattern changed shape, which made the experiment particularly convincing.”

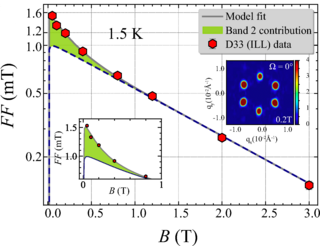
Magnetic field dependence of the measured quantity FF (first order vortex lattice form factor) highlighting the contribution of a second band. The inset on the right show example diffraction patterns measured at the instrument.

With a pure, high-quality sample – previously used for spectroscopy experiments by Karin Schmalzl and Arno Hiess, instrument scientists at the ILL – the same SANS technique was applied to 2H-NbSe₂. “We very quickly saw that 2H-NbSe₂ was behaving in exactly the same way as MgB₂: there was an almost identical suppression of one band, leaving only the second band contributing to the overall superconducting state,” explains Alshemi. The findings were confirmed by additional data acquired at SINQ, that expanded the range of temperatures and magnetic fields studied. The combined results, recently published in Physical Review Letters, highlighted as an ‘Editor's Suggestion’ and featured in Phys.org, prove the two-band superconductivity of 2H-NbSe₂. “Although the transition temperature of 2H-NbSe₂ (6.95K, -266^oC) is lower than that of MgB₂, our findings provide direct experimental confirmation of two-band superconductivity in 2H-NbSe₂, advancing our understanding of multiband superconductivity in the material and highlighting the broader relevance of such phenomena beyond high transition temperature considerations,” explains Alshemi.

The demonstration of two-band superconductivity in a second material also now confirms monochromatic SANS as the definitive go-to method to characterise multiband superconductivity in a material, in addition to the strength of continuous neutron sources for this area of research. “At the ILL, the experiments were carried out on the D33 instrument which has two modes: monochromatic, using one wavelength, and time-of-flight which uses a range of wavelengths,” explains Cubitt. “For this type of experiment, the monochromatic mode enables the neutron wavelength and angle to be tuned such that every neutron contributes to the Bragg peaks.” In contrast, at pulsed neutron sources, equivalent to the time-of-flight mode, the vast majority of neutrons would measure nothing and only contribute noise, making such an experiment certainly more difficult and less efficient.

The powerful monochromatic beam at the ILL will be equally crucial for the next phase of experiments that aim to investigate a number of intriguing physical phenomena speculated to exist in 2H-NbSe₂. “In my opinion, the D33 instrument at the ILL offers an impressive platform to probe and better understand such properties in 2H-NbSe₂ and other superconductors,” concludes Alshemi.

Reference: Alshemi, A. and Forgan, E. M. and Hiess, A. and Cubitt, R. and White, J. S. and Schmalzl, K. and Blackburn, E. 'Two Characteristic Contributions to the Superconducting State of 2H-NbSe₂', Phys. Rev. Lett., 134, 11 (2025).

doi.org/10.1103/PhysRevLett.134.116001

ILL instrument: D33

ILL contact: Bob Cubitt

Quantum mechanics, energy bands and superconductivity

In quantum mechanics, electrons (and other particles) behave both as particles and waves and have somewhat weird properties. In atoms, the energy of electrons is quantised (meaning that it can only have certain, discrete values) and their location is described by atomic orbitals (that can be used to calculate the probability of finding the electron in a specific region around the nucleus). In a large lattice of atoms or molecules, the band structure describes the range of energy levels that electrons may have. There are also band gaps - the ranges of energy that they may not have. Band theory derives these bands and gaps from the overlapping of electron orbitals.

In a "normal" conductor, electrons constantly collide with the ions in the lattice and a part of the energy transported in the current is lost - this corresponds to electrical resistance. In superconducting materials there is a temperature (critical temperature Tc) below which electric current can circulate without resistance, and thus without energy loss. These materials also expel magnetic fields as they transition to the superconducting state. The theory of superconductivity tells us that below Tc electrons form bound pairs (so-called Cooper pairs) due to a an attractive force between electrons in the lattice (caused by the interactions of electrons with atomic-level vibrations of the positively-charged lattice known as phonons). At higher temperatures, these very weak bounds are broken by the thermal vibrations of the lattice. Collectively the pairs can move through the material without resistance. This Cooper pair fluid has a specific energy band (and energy gap). Multiband superconductivity arises when multiple electronic bands contribute to the formation of the superconducting state, allowing distinct pairing interactions and gap structures.

Superconductivity was discovered over a century ago in mercury (and then in other metals and metal alloys) cooled to temperatures just a few degree above absolute zero (using liquid helium, at about -452°F). More recently, some decades ago, a news class of materials that are superconducting at (still low but) much higher temperatures - in some cases above liquid nitrogen (-321°F). Interestingly, the theory that describes superconductivity in metals and alloys does not apply to most of these new materials.