GBasireps

The program GBasIreps is a front-end intended to be used with the command line "BasIreps"

The program BasIreps calculates the irreducible representations (irreps) of the so called "little groups" from which the full irreducible representations of space groups can be calculated using the induction formula.

The method used in BasIreps for calculating the irreps is based in the procedure used in the program KAREP by E. Hovestreydt, I. Aroyo et al, J.Appl.Cryst. 25, 544 (1992). The method of Zak used in KAREP has been implemented in a special subroutine within BasIreps.

After calculating the irreps corresponding to a given space group and propagation vector the program calculates the basis functions corresponding to vectorial properties (atom displacements or magnetic moments) of atoms in crystalline solids.

This program calculates non-normalized basis functions of the irreducible representations of the little group Gk for atom properties in a crystal.

In particular for atomic displacements (or phonon modes) as polar vectors and magnetic moments as axial vectors. In general the displacement/magnetic moment of atom j in cell L may be written as a Fourier series of the form:

k and R are vectors referred to the reciprocal and direct crystallographic basis respectively.
The vectors m(j,L) and S(j,k) have the same units and are referred to a basis of unit vectors along the direct crystallographic cell basis.
S(j,k) are the Fourier components of the magnetic moments (or displacements) m(j,L).

Taking into account the symmetry, the vectors S(j,k) may be written as linear combinations of the so-called basis functions of the irreducible representations of the propagation vector group Gk.

The number of free parameters in a displacive phase transition, or in a magnetic structure, is less than N=3 x n x O{k}.
The number 3 comes from the three components of S(j,k), n is the total number of atoms in a primitive cell and O{k} is the number of propagation vectors.
The number of independent free parameters (order parameters) can be calculated from group theory. In general the vector S(j,k) may be written as:

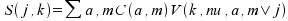
where C(a,m) are the coefficients (that may be real or pure imaginary) of the linear combination, and V(k,nu,a,m|j) are constant vectors referred to the basis of the direct cell.

The labels are the following (k,nu) is for the particular propagation vector and the representation called Gamma(nu).

The index 'a' varies from 1 up to the dimension of the irreducible representation: a=1,2,...dim(Gamma(nu)).
The index m varies from 1 to the number of times the irreducible representation Gamma(nu) is contained in the global mechanic/magnetic reducible representation constructed by working with the symmetry operators acting on atoms coordinates and components of polar/axial vectors (dimension 3 x n).
See, for instance, the book by Y.A. Izyumov, V.E. Naish and R.P. Ozerov (1991) for details.

The program BasIreps calculates the vectors V(k,nu,a,m|j) in a non-normalized form.
However, the final form of the basis functions are written as simple as possible.
An effort in future versions will be performed to recognize particular combinations of common numbers.

Screenshots:

• GBasireps screenshot #1