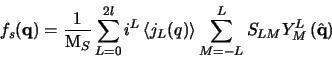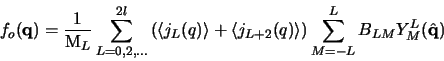

Next: Analytical approximation
Up: Magnetic Form Factors
Previous: Magnetic Form Factors
The magnetic form factor
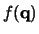 is obtained from the fourier transform of
the magnetisation distribution of a single magnetic atom. Assuming that it
has a unique magnetisation direction it can be written
is obtained from the fourier transform of
the magnetisation distribution of a single magnetic atom. Assuming that it
has a unique magnetisation direction it can be written
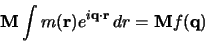 |
(1) |
where M gives the magnitude and direction of the moment and
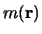 is
a normalised scalar function which describes how the intensity of magnetisation
varies over the volume of the atom.
When the magnetisation arises from electrons in a single open shell the magnetic
form factor can be calculated from the radial distribution of the electrons in
that shell. The integrals from which the form factors are obtained have the form
is
a normalised scalar function which describes how the intensity of magnetisation
varies over the volume of the atom.
When the magnetisation arises from electrons in a single open shell the magnetic
form factor can be calculated from the radial distribution of the electrons in
that shell. The integrals from which the form factors are obtained have the form
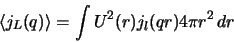 |
(2) |
The jl are the spherical Bessel functions defined by
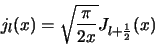 |
(3) |
If the open shell has orbital quantum number l the form factor
for spin moment is
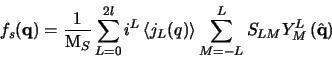 |
(4) |
and that for orbital moment
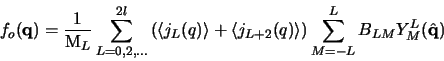 |
(5) |
The coefficients SLM, BLM have to be computed from the orbital
wave-function [1]. The total spin moment
MS is
given by S00
and the orbital moment
ML by B00. For small q the dipole
approximation
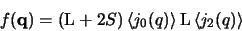 |
(6) |
can be used.


Next: Analytical approximation
Up: Magnetic Form Factors
Previous: Magnetic Form Factors
P.J. Brown - Institut Laue Langevin, Grenoble, FRANCE. e-mail: brown@ill.fr